Solution——BIP032
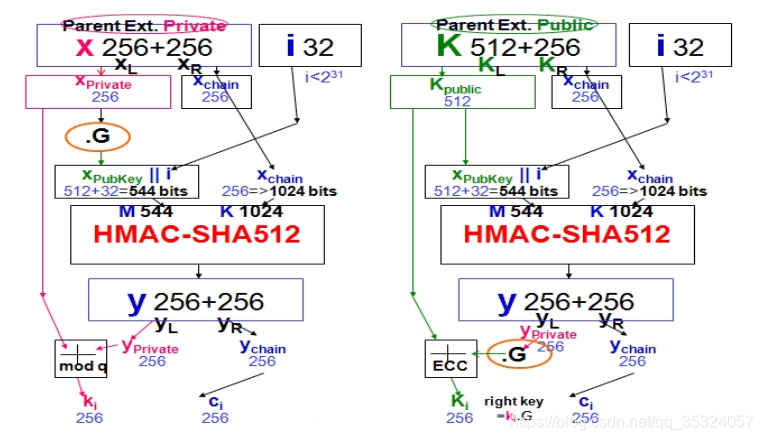
当$i\geq2^{31}$时,我们称之为硬化子秘钥衍生,如下图: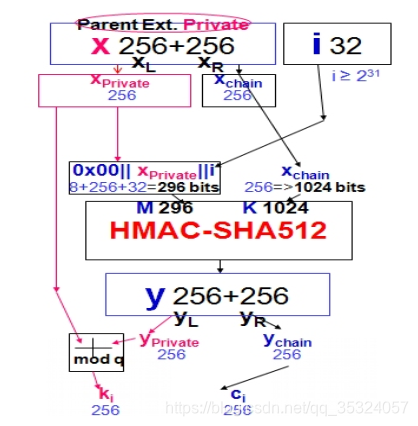
对于solution1,如果我们知道扩展私钥$k_1$,并且知道该私钥的相对位置,那么我们可以通过$K,xc$(链码)计算得到$y_1、y_2$,由于:$y_1k \, mod \, q=k_1$,所以我们可以解出$k$,进而可以计算出:$y_2k\, mod \,q=y_2$,依次类推进而计算出所有的私钥。同理可证solution2。
攻击
如果攻击者知道$Extended\:Public\:Key\:K||xc$并且相同的随机数被处在同一层中的两个用户使用了,知道他们的相对路径,那么可以计算出对应的:$y_L$,我们假设用户1对应的是:$y_1$,用户2对应的是:$y_2$所以两个对应的私钥就是:$ky_1、ky_2$,得到:
$as_1=(H(m1)+rky_1)\,mod\,q$
$as_2=(H(m2)+rky_2)\,mod\,q$
将第一个等式中的$a$表示出来带入第二个等式得到:
$k=\frac{H(m2)s_1-H(m1)s_2}{ry_1s_2-ry_2s_1}mod\:q$
这样我们就可以解得私钥的值。
如果攻击者知道两个不同层次的:$K,xc$以及用户的相对位置,并且随机数$a、b$都各自使用了一次,一共有四个用户。
对于solution1因为我们知道用户的相对位置,我们可以计算出:$ky_1,k’y_2,ky_3,k’y_4$并且得到如下几个式子:
$as_1=(H(m1)+r_aky_1)\,mod\,q$
$as_2=(H(m2)+r_ak’y_2)\,mod\,q$
$bs_3=(H(m3)+r_bky_3)\,mod\,q$
$bs_4=(H(m4)+r_bky’_1)\,mod\,q$
$ky_1s_2-k’y_2s_2=\frac{H(m_2)s_1+H(m1)s_2}{r_a}mod\,q$
$ky_3s_4-k’y_4s_3=\frac{H(m_4)s_3+H(m3)s_4}{r_b}mod\,q$
两个方程可以解出$k$和$k’$,与之前类似的方法即可解出所有私钥。solution2同理。